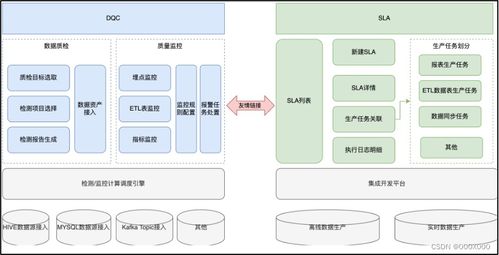
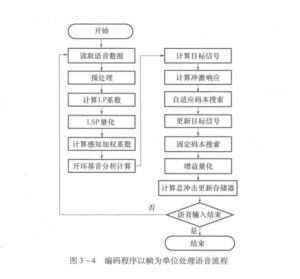
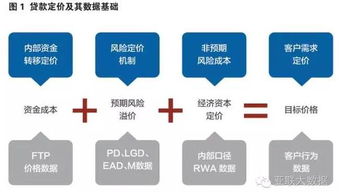
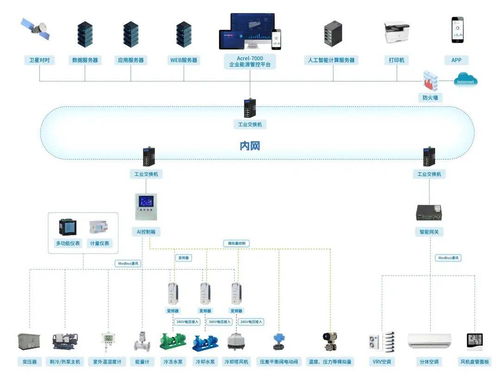
數據結構和算法中的圖 基礎軟件服務的核心支柱
在計算機科學的世界里,數據結構與算法是構建一切軟件應用的基石。其中,“圖”(Graph)作為一種極其重要且強大的數據結構,在當今的基礎軟件服務中扮演著不可或缺的角色。它不僅是一種抽象的數學概念,更是解決復雜現實問題的關鍵工具。
一、 圖的基本概念
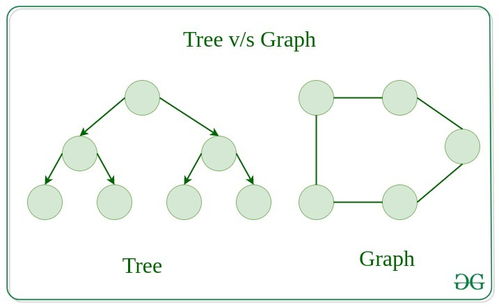
圖是由“頂點”(Vertex或Node)的集合和連接頂點的“邊”(Edge)的集合組成的數據結構。它可以形式化地表示為 G = (V, E),其中 V 代表頂點集,E 代表邊集。根據邊的性質,圖主要分為兩大類:
1. 無向圖:邊沒有方向,表示頂點間雙向的關系(如社交網絡中的好友關系)。
2. 有向圖:邊有方向,表示從一個頂點到另一個頂點的單向關系(如網頁間的超鏈接、任務間的依賴)。
邊還可以有權重,構成“帶權圖”,用于表示連接的成本、距離或強度(如地圖中城市間的距離、網絡帶寬)。
二、 圖的算法與應用
圖的強大能力通過一系列經典算法得以釋放,這些算法是許多基礎服務的引擎:
- 遍歷算法:深度優先搜索(DFS)和廣度優先搜索(BFS)是探索圖結構的基礎。BFS常用于尋找最短路徑(在邊權相等時),DFS則在拓撲排序、檢測環路中發揮關鍵作用。
- 最短路徑算法:如迪杰斯特拉算法(Dijkstra)和弗洛伊德算法(Floyd),它們為導航軟件(如谷歌地圖、高德地圖)提供核心路徑規劃能力,計算兩點間最快或最短的路線。
- 最小生成樹算法:如普里姆算法(Prim)和克魯斯卡爾算法(Kruskal),用于在保證所有節點連通的前提下,以最小總成本構建網絡。這在通信網絡布局、電路設計等領域至關重要。
- 拓撲排序:針對有向無環圖,將頂點排成一個線性序列。這是軟件構建工具(如Make, Maven, Gradle)解析項目依賴關系、確定編譯順序的核心。
- 連通性與社區發現:通過算法尋找圖中的連通分量或密集子圖,是社交網絡分析、推薦系統識別興趣群體、網絡安全檢測異常集群的基礎。
三、 圖在基礎軟件服務中的核心地位
基礎軟件服務,如操作系統、數據庫、網絡服務和中間件,廣泛依賴圖模型來解決其內部和外部的復雜關系問題。
- 網絡與分布式系統:互聯網本身就是一個巨大的圖。路由器使用圖算法進行路由尋址;內容分發網絡(CDN)利用圖論優化資源部署;分布式數據庫(如Neo4j等圖數據庫)更是直接以圖作為數據模型,高效處理高度關聯的數據。
- 社交網絡與推薦引擎:Facebook、LinkedIn等平臺將用戶和關系建模為圖,使用圖算法進行好友推薦、信息流排序和影響力分析。
- 搜索引擎:谷歌的PageRank算法本質上是一個運行在由網頁和超鏈接構成的巨大有向圖上的算法,通過分析鏈接關系來確定網頁的重要性排名。
- 編譯器和軟件開發工具:程序代碼可以被抽象為抽象語法樹(一種特殊的圖)和控制流圖,編譯器利用圖算法進行代碼優化、死代碼消除和數據流分析。
- 網絡安全與欺詐檢測:通過將交易、IP地址、設備等信息構建成圖,可以識別出異常的連接模式和欺詐團伙,這是金融科技和網絡安全領域的關鍵防御手段。
###
總而言之,圖作為一種高度靈活和表達力強的數據結構,配合其豐富的算法庫,已經成為支撐現代基礎軟件服務的中樞神經。從我們指尖滑動的社交應用到背后龐大的云計算基礎設施,圖的理論與應用無處不在。深入理解圖數據結構與算法,不僅是計算機科學教育的核心,更是設計和優化下一代高性能、智能化的軟件服務的必備技能。
如若轉載,請注明出處:http://www.pocou.cn/product/56.html
更新時間:2026-02-10 00:51:00